Research
I am broadly interested in combinatorial algebraic geometry. Most of my work is in positive geometry, which studies semi-algebraic subsets of real algebraic varieties defined by natural positivity conditions. The Ur-example is the positive Grassmannian, and other examples include polytopes, the moduli space of points on a line, and positive parts of many homogeneous spaces. This is a relatively new field of math inspired by computations in scattering amplitudes.
Click on the triangle by each paper for a summary.
Papers
Avoidance Loci of Real Projective Varieties (preprint, with Ada Wang)
We define the avoidance locus to consist of real linear spaces intersecting a real projective variety at no real point. This generalizes the cone of positive polynomials, which consists of hyperplanes avoiding the Veronese variety. We prove that the avoidance locus is a union of non-adjacent regions in the complement of a higher Chow form.
.
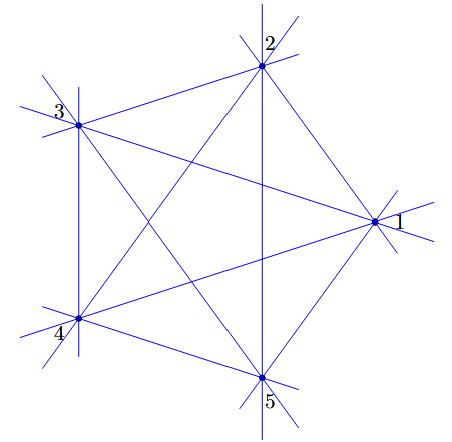
Exterior Cyclic Polytopes and Convexity of Amplituhedra (preprint, with Elia Mazzucchelli)
We show that the k=m=2 amplituhedron is the intersection of Gr(2,4) with a polytope, which we call the exterior cyclic polytope. Furthermore, we described the dual of this polytope in terms of the twist map of Marsh and Scott, and use this to define a notion of dual amplituhedron.
.
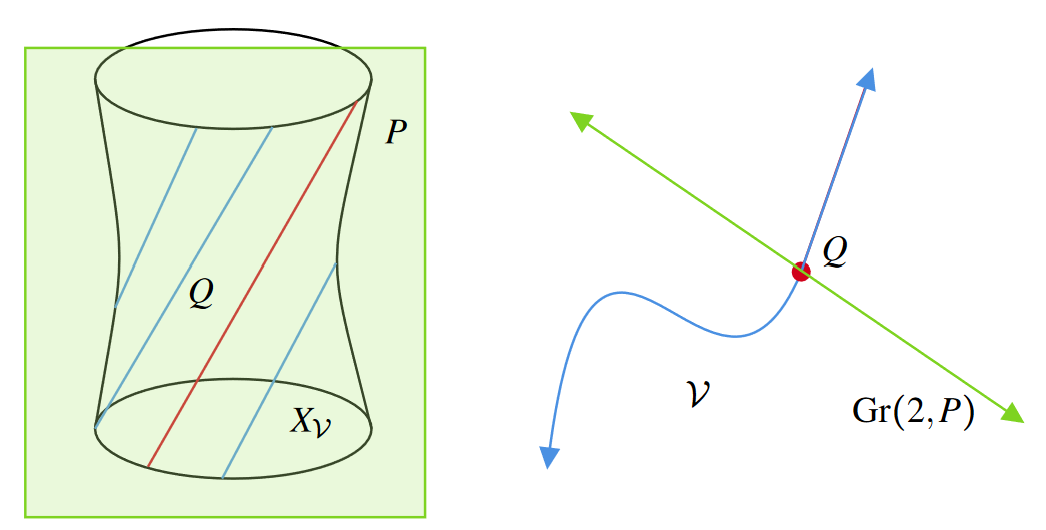
The Segre Determinant (preprint)
The Segre determinant is a polynomial which encodes the condition for points to lie on a bilinear hypersurface in the product of projective spaces. We show that the Segre determinant represents the Chow-Lam form of a generic torus orbit in the Grassmannian, and gives some applications to algebraic vision and to Chow quotients of Grassmannians.
.
FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI (preprint, with many co-authors)
I contributed some problems to this problem bank, which serves as a benchmark for evaluating AI performance. The paper explains the methodology in more detail and evaluates several leading models on this problem set.
.
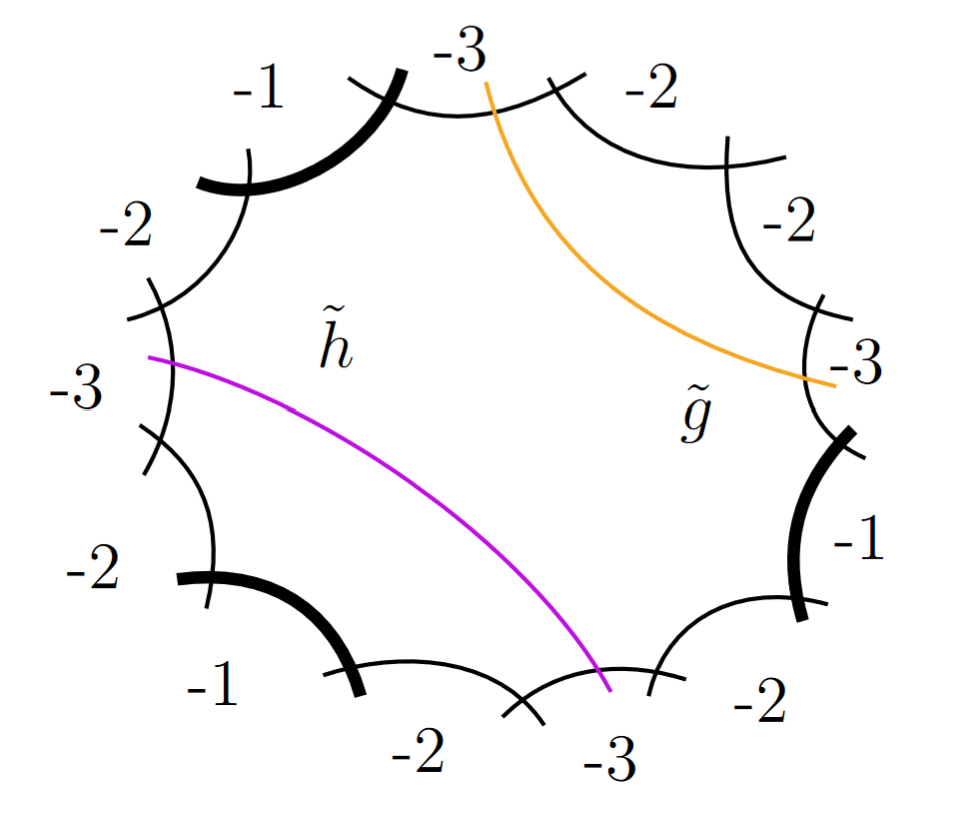
Chow-Lam Recovery (Le Matematiche 2025, with Kristian Ranestad)
We explore the extent to which a subvariety of the Grassmannian can be uniquely recovered from its Chow-Lam form. Unlike the classical case of Chow forms for projective varieties, this is not always possible, and we provide several interesting families of counter-examples.
.
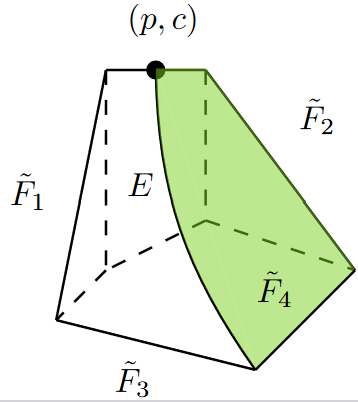
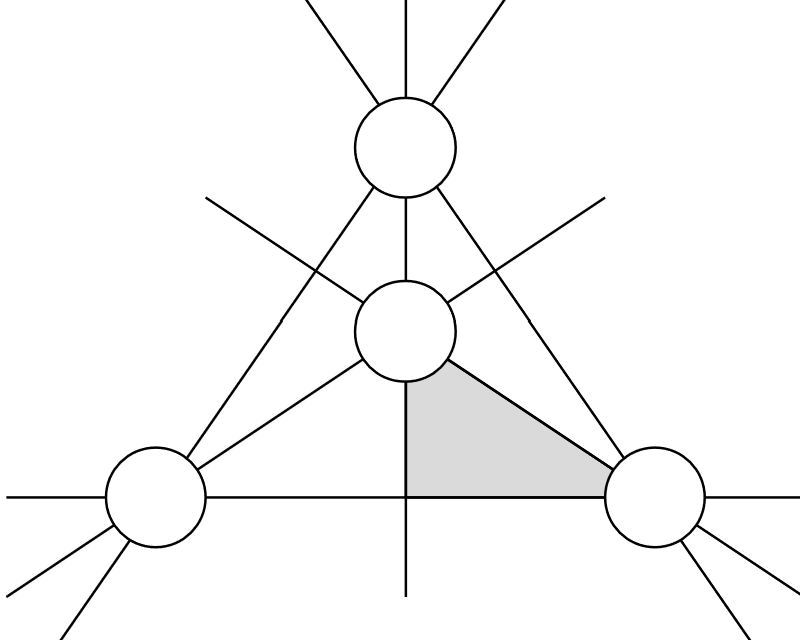
Wondertopes (Advances in Math 2025, with Sarah Brauner, Chris Eur, and Raluca Vlad)
We provide a new type of positive geometry called a wondertope (wonderful polytope). It is constructed by pulling back an open region of a hyperplane arrangement to the wonderful compatification of the arrangement, then taking the Euclidean closure.
The Chow-Lam Form (Journal of Symbolic Computation 2025, with Bernd Sturmfels)
We introduce the Chow-Lam form for subvarieties of the Grassmannian, generalizing the classical Chow form. This gives us universal formulas for projections between Grassmannians and their branch loci.
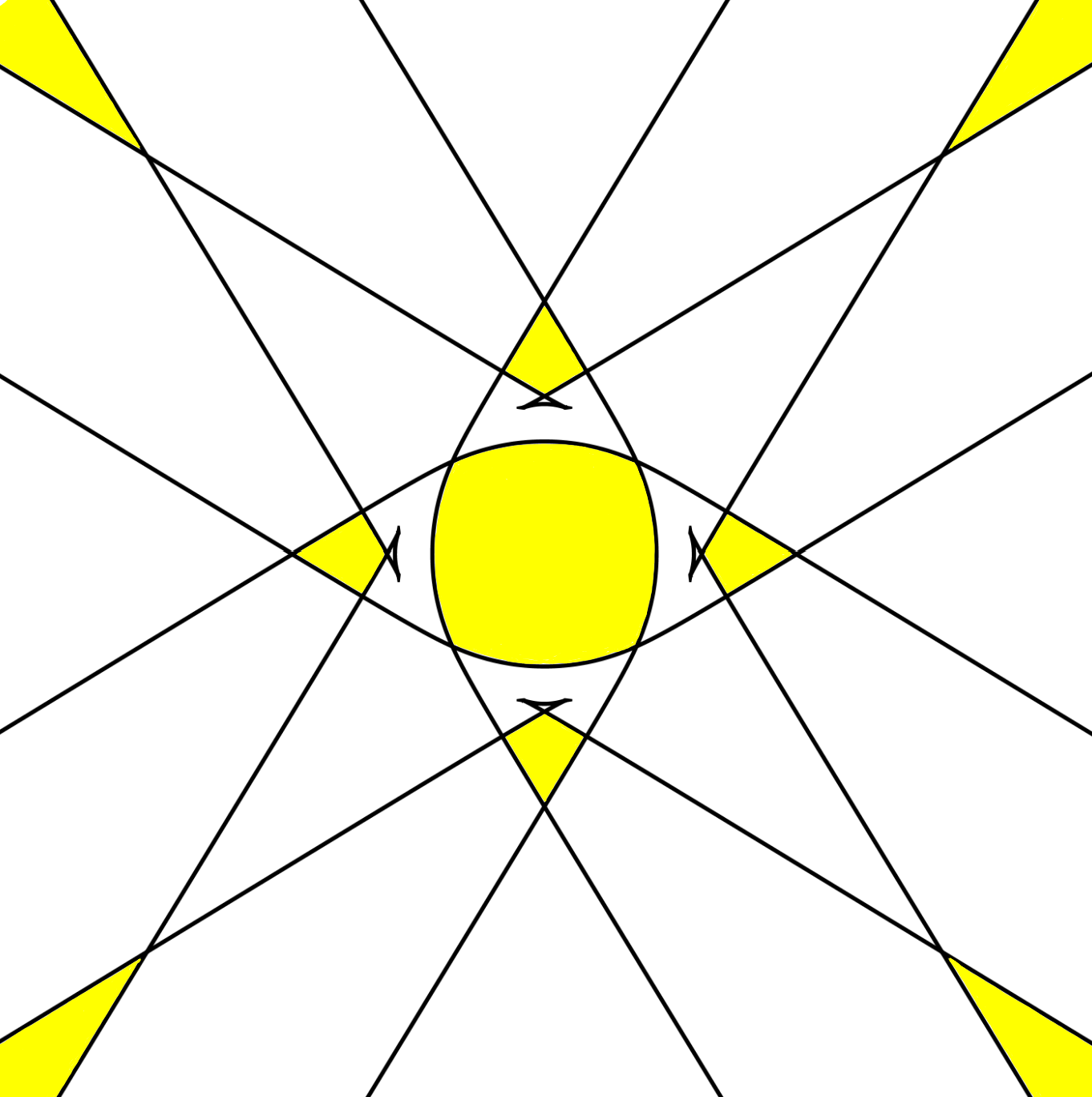
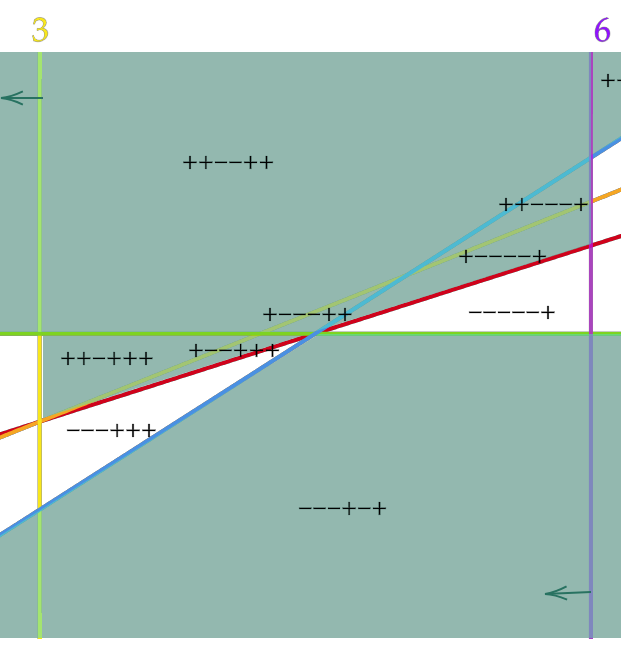
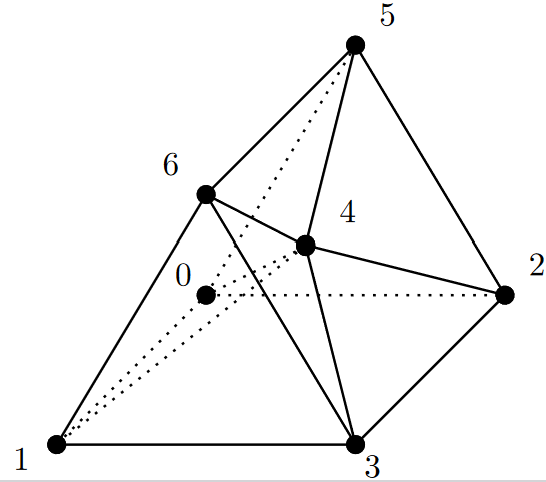
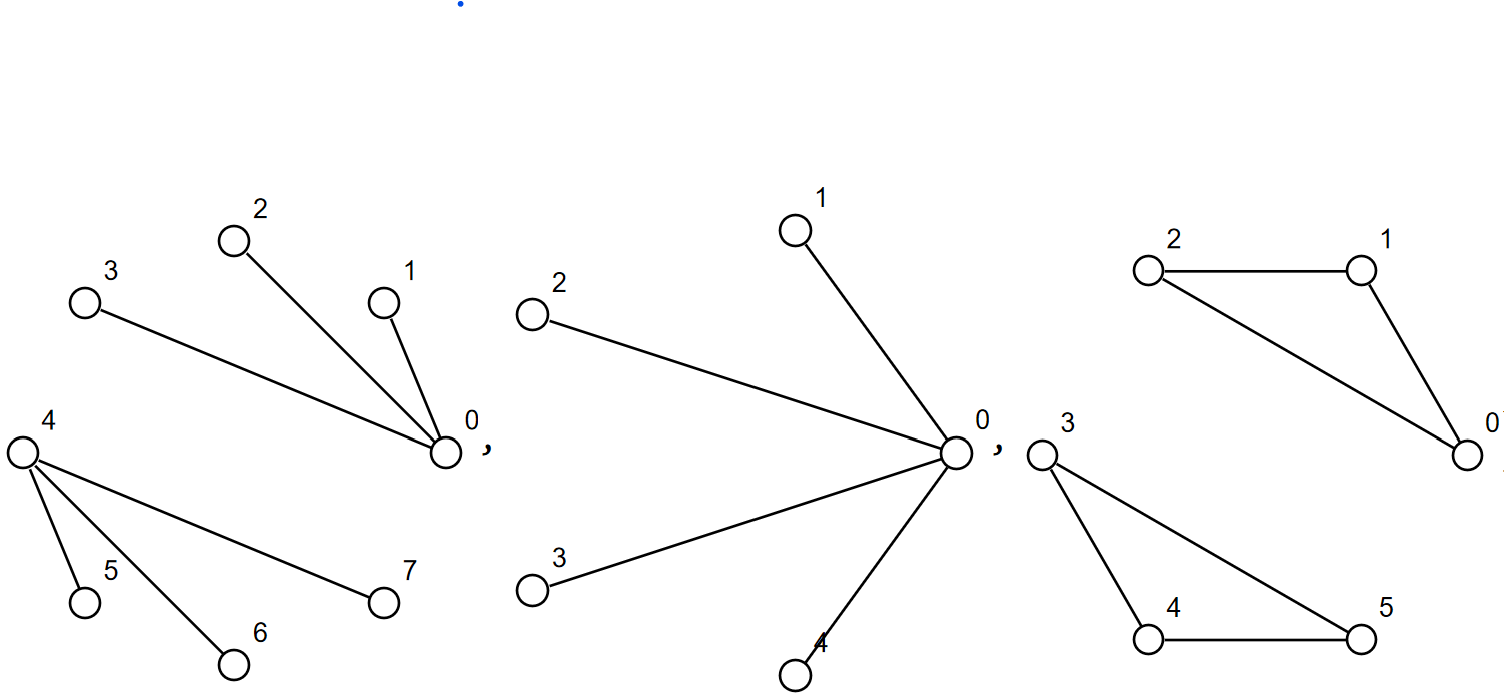
Combinatorics of m=1 Grasstopes (Journal of Combinatorial Theory , with Yelena Mandelshtam and Dmitrii Pavlov)
Grasstopes are a generalization of amplituhedra. Building on work of Karp and Williams on the m=1 amplituhedron, we show that m=1 Grasstopes consist of regions of a hyperplane arrangement characterized by a sign condition.
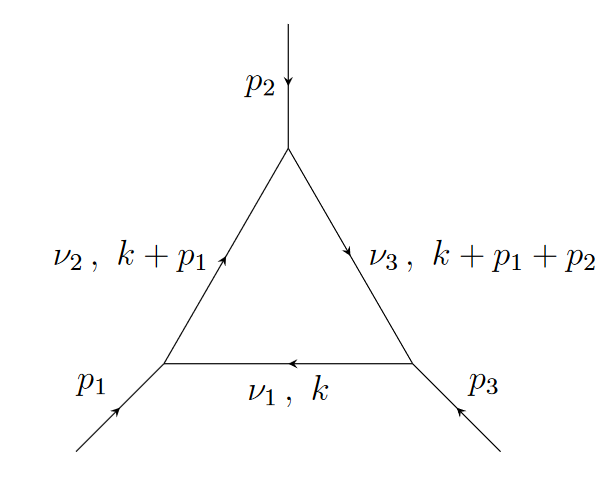
D-Module Techniques for Solving Differential Equations in the Context of Feynman Integrals (Letters in Mathematical Physics> 2024, with Johannes Henn, Anna-Laura Sattelberger, and Simone Zoia)
We use D-module methods to construct series solutions to linear differential equations appearing in the context of Feynman integrals.
On the Geometry of Elliptic Pairs ( Journal of Pure and Applied Algebra 2023)
In this paper we classify toric elliptic pairs of Picard number two. These elliptic pairs are used to construct examples of surfaces whose pseudo-effective cone is non-polyhedral for a set of primes of positive density, and, assuming the generalized Riemann hypothesis, polyhedral for a set of primes of positive density.
Quantum Jacobi forms and sums of tails identities (Research in Number Theory 2022, with Amanda Folsom, Noah Solomon, and Andrew Tawfeek)
We discover new examples of hypergeometric series which are quantum Jacobi forms, i.e. satisfy a modular transformation property up to an analytic error term.